Maximum Likelihood Histogram Probabilistic Multi-Hypothesis Tracker
A new target tracking algorithm for detecting and tracking low SNR targets in dense debris environments
We have developed a new target tracking algorithm capable of detecting, tracking, and determining the number of very low signal-to-noise ratio (SNR) targets—if necessary, unresolved ones—in high noise or densely cluttered environments. This new algorithm is a game changer in the passive sensor tracking arena. The Maximum Likelihood, Histogram Probabilistic Multi-Hypothesis Tracker (ML-HPMHT) is showing very promising and robust results. We believe that for the extraction of extremely low-observable targets with parametrizable motion, the ML-HPMHT is better than any other existing algorithm.
Conventional approaches to this problem, which involve thresholding, measurement detection, data association, and filtering, encounter problems due to target energy being spread across multiple cells of the IR imagery. Thus, the Multiple Hypothesis Tracker (MHT), Global Nearest Neighbor (GNN), and even particle filters (PF) that rely on thresholded data suffer from the underpinning logic that at most one measurement originates from one target. This cannot be improved by pre-processing masks, filters, or other methods to reduce the amount of noise or debris in the background environment.
A histogram based probabilistic multi-hypothesis tracking (HPMHT) approach provides an automatic means of modeling targets that are spread across multiple pixels of the focal plane array (FPA) by relaxing the need for hard decisions on measurement detection and data association. Furthermore, we generalize the conventional HPMHT by adding an extra layer of EM iteration that yields the maximum likelihood (ML) estimate of the number of targets, thereby creating the ML-HPMHT algorithm.
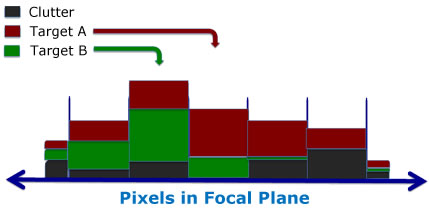
This figure shows the energy in each pixel in the FPA. The detector of course sees only the sum of the energies, but in this clairvoyant figure we can see it broken down into its component parts. We can even see the locations of the targets before these are smeared by their point spread functions (PSFs).
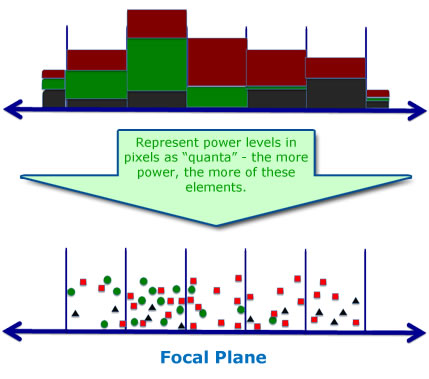
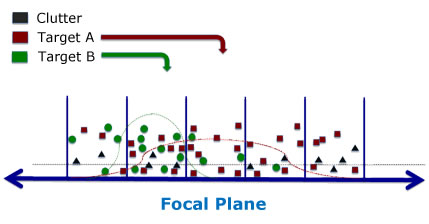
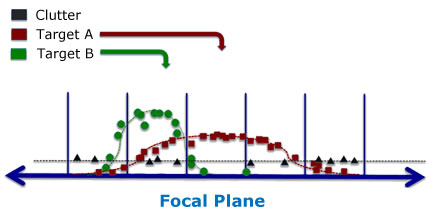
The EM recursion operates to estimate the locations and widths of the target spreads – these are the "desired" variables that are sought. However, the "hidden" data includes both the labels of the quanta and their positions within the bins, and the EM iteration finds the posterior probabilities of both of these. Perhaps surprisingly, treating the locations as hidden actually simplifies the problem!
Download the ML-HPMHT brochure (.pdf, ~350kb)


